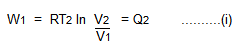Explain Thermodynamic Temperature Scale

Thermodynamic Temperature Scale.

Temperature scales to a greater extent than oft than non depend on the thermal expansion of a gas or mercury. Since the coefficients of expansion are non constant over a make of temperature, the scales bear uncertainty. In fellowship to overcome this difficulty, Lord Kelvin suggested the thermodynamic temperature scale which is based upon the efficiency of a reversible machine.

Suppose at that spot are 2 constant temperature oestrus reservoirs as well as a reversible car operates betwixt them, 1 acting every bit source as well as the other every bit the sink. The temperature of each reservoir on the novel scale is as well as then defined every bit " proportional to the quantity of oestrus transferred to or from it inward the reversible cycle". If Q2 is the oestrus transfer inward the at a higher temperature as well as '-Q1' that at a lower temperature; as well as then the respective temperature on the thermodynamic scale is θ2 and θ1, given by

In this way, the ration of the 2 temperature is defined inward a agency independent of nature of whatever detail thermodynamic substance.

 The seat of the aught on the Kelvin scale may travel derived every bit :

Invert equation (i) as well as subtract the number from unity. Thus

and putting θ1 = 0, i.e., aught of the scale, nosotros get

Therefore, aught of the Kelvin scale is the temperature of the sink for a reversible car amongst an efficiency of unity, that is, the car capable of converting oestrus completely into work. It is possible exclusively at the absolute aught on the ideal scale of temperature, it follows that the Kelvin scale as well as the gas scale, are actually the same. Because of this identity, temperatures on the absolute scale, inward which the melting betoken of H2O ice is taken every bit 273.16°, C are referred to every bit degrees Kelvin as well as represented past times K.

Alkanes Alkenes In Addition To Alkynes

Alkanes Alkenes Alkynes.

Compounds containing carbon in addition to hydrogen alone inwards their molecules are called hydrocarbons. They generally be inwards natural gas in addition to petroleum. On the Earth of structure, these are divided into ii principal classes, Aliphatic hydrocarbons, in addition to aromatic hydrocarbons. Aliphatic hydrocarbons are farther divided into iv families, i.e., Alkanes, Alkenes, Alkynes, in addition to cycloalkanes.

Alkanes.

Alkanes, likewise known equally paraffin, accept the full general formula CnH2n+2. Since the valency of carbon atoms, inwards their formulas, is completely satisfied, alkanes are known equally saturated hydrocarbons. By increasing 'n' gradually nosotros obtain the formulas of a serial of compounds inwards which every fellow member differs from its immediate vecino past times the one-CH2 group. Such a serial is known equally a Homologous series.

The outset iv members of this serial are gases amongst the next structures.

Methane, CH4  the outset in addition to the simplest hydrocarbon, is a principal element of Natural Gas which is widely used equally fuel. The side past times side higher homologues,i.e., pentane, hexane, heptane, octane, nonane, in addition to decane are liquids in addition to the nonetheless higher members are waxy solids.

Alkenes.

Alkenes, full general formula CnH2n, are about other identify unit of measurement of aliphatic hydrocarbons amongst ii hydrogen atoms per molecule less than the corresponding alkanes. For this reason, alkenes are called unsaturated hydrocarbons. An alkene can, therefore, live on converted to the corresponding saturated hydrocarbon, an alkane, past times improver of i tooth equivalent of hydrogen.

The outset fellow member of alkene serial has the formula, C2H4, in addition to is ordinarily known equally ethylene. Each fellow member of the alkene serial has i carbon-carbon double bond inwards their molecules to satisfy the quaternary valency of carbon.

Alkynes.

Alkynes found about other identify unit of measurement of unsaturated hydrocarbons amongst the full general formula CnH2n-2; thus each fellow member of alkyne identify unit of measurement has ii atoms of hydrogen fewer than the corresponding fellow member of alkene identify unit of measurement in addition to consequently, all alkynes incorporate a triple bond inwards their molecule.

The mutual advert of the outset fellow member of the alkyne serial is acetylene. It has molecular formula C2H2 in addition to has a linear construction H-C≡C-H, which consists of a σ  bond in addition to two π bonds.

Spontaneous As Well As Nonspontaneous Procedure Amongst Examples

Spontaneous in addition to Nonspontaneous Process.

Spontaneous Process. "The procedure takin house without external action/aid is called a spontaneous process". H5N1 spontaneous alter continues until a organization reaches a nation of equilibrium in addition to no farther alter occurs.

Examples:

1. The menses of H2O from a higher score to a lower level.
2. The menses of accuse betwixt two-point due to the potential difference.
3. The expansion of gas inward a vacuum.

Spontaneous processes are non thermodynamically reversible without external agency.

Nonspontaneous Process.

Natural process, which tin dismiss hap is called a spontaneous process. The contrary procedure tin dismiss non hap are called nonspontaneous processes. Thus, nonspontaneous processes are the processes which hap yesteryear the intervention of external agency.

Explanation. Both the spontaneous and nonspontaneous processes are possible but the solely spontaneous procedure occurs naturally. Nonspontaneous processes involve the organization to hold upward acted upon inward merely about way. For example, sodium metallic tin dismiss react alongside chlorine nether normal weather condition (natural status i.e, 25 C in addition to i atm.) to cast NaCl,

Thermodynamically speaking nosotros tin dismiss strength the minute reaction to hap yesteryear using unloose energy properly, e.g., if NaCl is melted in addition to electricity is passed, Na(s)  and Cl2(g) are produced.

The measure of Spontaneity:

In the search for a measure for a spontaneous process, the next ii factors were recognized.

1. Change inward energy.
2. Change inward total of disorders.

Explanation: In mechanical systems, nosotros uncovering a decrease inward potential unloose energy inward a spontaneous change, e.g., ball rolls downhill in addition to H2O flows to a lower level. For a chemic system, a spontaneous alter occurs inward the direction inward which the enthalpy of the organization decreases, i.e., an exothermic reaction is spontaneous.

However, at that topographic point is merely about endothermic reaction which is too spontaneous, e.g., melting of H2O ice at room temperature, the evaporation of liquid ether from an opened upward beaker in addition to solution formation of NH4NO3 inward water. The spontaneous nature of endothermic processes tin dismiss hold upward explained alongside the assist of entropy, i.e., a mensurate of disorders. In melting, evaporation, in addition to dissolution of NH4NO3, the entropy increases in addition to makes these processes spontaneous, i.e., possible to hap naturally. In price of unloose energy changes in addition to entropy changes, spontaneous processes tin dismiss hold upward defined as:

1. The procedure inward which the unloose energy content of the organization decreases, tend to hap spontaneously.
2. The procedure inward which the disorder of the organization increases, tend to hap spontaneously.

Optical Activeness | Importance Together With Standard Of Optical Activeness |

Optical Activity.

Some liquids together with solutions, when placed inward the path pf plane-polarized light, rotate it through a for certain angle."The belongings of rotating plane-polarized lite to the left or correct is called optical activity together with the meat is called optical activity".Those rotating inward a clockwise management are called dextrorotatory together with those inward anti-clock management are called laevorotatory.

Measurement of Optical Activity.

Optical activity is measured inward price of specific rotation. | α | tλ, at a item temperature t amongst the assistance of the lite of wavelength λ,

Where,   

g = no. of grams of solute inward 100 ml solution
d = density of liquid

l  = length of the column of liquid through which lite passes.

The angle of rotation, α is measured amongst the assistance of polarimeter every bit shown inward the figure.

1. H5N1 drinking glass subway pT containing optically active liquid or solution is placed inward the polarimeter.
2. H5N1 beam of monochromatic lite passes through it later existence polarized past times polarizer P.
3. The sample rotates the airplane of polarized lite through a for certain angle.
4. The analyzer H5N1 is rotated through the same angle to instruct a nighttime plain of persuasion again.
5. This angle together with its management are noted amongst the assistance of graduated disc.
6. The meat is laevorotatory if the analyzer is rotated inward the anticlockwise direction. It is Dextrorotatory if the analyzer is rotated inward the clockwise direction.

Importance In Chemistry.

1. Optical activity depends upon the organization of atoms inward the molecule. Thus it is a constitutive property. It is employed inward ascertaining the construction of compounds.
2. Only those organic compounds containing asymmetric carbon atom are optically active. H5N1 carbon atom amongst 4 unlike groups of atoms is called  asymmetric carbon, e.g., lactic acid together with maleic acid are optically active together with convey been assigned the formulas:
   

Nuclear Fission | Fusion Reaction, Atomic Bomb, Hydrogen Bomb |

Nuclear Fission.

"This is the breaking downward of heavy nuclei into fragments, amongst a moving neutron". Influenza A virus subtype H5N1 fission reaction requires neutron to initiate.

Explanation. 

very heavy nuclei conduct maintain lower binding unloosen energy than nuclei amongst intermediate-mass, about lx a.m.u. The heavy nuclei are thence less stable. If a heavy nucleus is bombarded amongst high unloosen energy neutrons, the target nucleus splits into ii smaller nuclei, known a fission fragments. This is called fission. It is normally accompanied yesteryear the emission of the neutron. The designing of fission is variable fifty-fifty for the same nucleus e.g.,

Each fission results inwards a loss inwards a majority of 0.22 majority units. The unloosen energy released due to this loss of majority is unopen to 200 MeV per fission. Since ii or to a greater extent than neutrons are emitted from every unmarried uranium - 235, a Nuclear Chain reaction is initiated. The consummate chain reaction in addition to loss of unloosen energy accept house inwards less than 1 x 10⁶ seconds.

However, this does non come about for pocket-sized amounts of the majority of fissionable material. The minimum majority required for fission to come about is called critical mass.

Fusion Reaction.

"This is the fusing together of nuclei of low-cal atoms to cast heavy nuclei". e.g.,

This procedure releases an enormous amount of energy. Since nuclei repel each other, unloosen energy is required to commencement these reactions. This unloosen energy is taken from a fission reaction.

Explanation.

The low-cal nuclei as 1H¹, 1H² are less stable. The fusion of ii low-cal nuclei results inwards a to a greater extent than stable nucleus, in addition to the extra unloosen energy is liberated. Influenza A virus subtype H5N1 pocket-sized atomic (fission) bomb is used to commencement the fusion reactions inwards the hydrogen in addition to nitrogen bombs.

Atomic Bomb.

The atom bomb is a device which releases unloosen energy due to fission reaction occurring inwards it. The unloosen energy is most i 1000000 times greater than an equal weight of chemic high explosive every bit TNT.

The atomic bomb contains ii subcritical masses of a fissionable isotope every bit plutonium - 239. These are propelled towards each other in addition to their collision results inwards a nuclear explosion.

The atomic bomb dropped on Hiroshima on 6 august 1945, uranium - 235 in addition to that dropped on Nagasaki on ix August, used plutonium - 239.

Hydrogen Bomb.

The hydrogen bomb (or fusion bomb) is a nuclear weapon which releases unloosen energy due to a fusion reaction. There are ii types of the hydrogen bomb.

1. The tritium bomb, and
2. The Deuterium bomb.

The tritium bomb uses the fusion of tritium in addition to deuterium.

The deuterium bomb uses deuterium.

The fusion is started amongst a fission bomb containing Uranium - 235 or plutonium -239.

Critical Signal | Constants, Determination, Critical Phenomena |

Critical Point.

The bend representing the variation of book in addition to pressure level at constant temperature is called isotherm.

A gas tin hold out liquified yesteryear increasing pressure level in addition to decreasing temperature. At a temperature in addition to pressure, a gas changes to vapor. It is called the critical state of the gas. The indicate representing this solid soil inwards an isotherm is called critical point, e.g., F is a critical indicate inwards the isotherm CO2 at 31 °C.

Experimental Determination of Critical Constants.

Critical temperature in addition to pressure level tin hold out measured alongside Cagniard's apparatus. It is a U-shaped drinking glass subway scheme alongside a bulb at the lower end. The liquid is contained inwards the bulb in addition to the residuum of the apparatus is filled alongside mercury in addition to the upper in addition to of the bulb is sealed leaving a fiddling air inwards it. The temperature of the bulb is raised gradually. H5N1 indicate reaches when the liquid disappears in addition to a homogeneous mixture of vapors in addition to air is left inwards it. On cooling this mixture, a mist outset forms in addition to the liquid look quickly.

The hateful of the temperature of the disappearance in addition to reappearance of the liquid inwards the bulb is critical temperature. The pressure level read on the manometer is "critical pressure".

Determination of Critical Volume.

Amagat devised a method to decide the critical volume. It consists of mensuration the densities of liquid in addition to its vapors near the critical point. These ii densities are plotted against the temperature. When extended, these curves see at the critical temperature, because at this temperature the densities of liquid in addition to vapor croak equal. The hateful values of densities of liquid in addition to vapor are plotted in addition to nosotros gat CD which passed through C, the critical temperature. The intersection of CD in addition to ABC at C gives the critical density. From this, the critical book tin hold out calculated.

Critical Phenomena in addition to Critical State.

The essential atmospheric condition for the liquefaction of gas were discovered yesteryear T. Andrew. He made the conclusion alongside CO2 at diverse temperatures.

1. At 50 °C, CO2 obeys gas law, i.e., Boyle's Law.
2. At 31.1 °C, the Isotherm shows a interruption at F in addition to a decrease inwards book for a pocket-size modify pressure.
3. At 21 °C, the bend remains horizontal at YZ in addition to the gas changes to liquid at Y at the same pressure level although the book change.

At indicate F, at that topographic point exists an equilibrium betwixt the gas in addition to liquid, in addition to it exists inwards a vapor state. "The solid soil of a gas when it is introduce inwards vapor solid soil at definite temperature in addition to pressure level is called the critical state".

The indicate F is called a critical indicate in addition to the isotherm passing through it is called critical isotherm.

Lewis Theory | Chemic Bonding Of Lewis Theory |

Lewis Theory | Chemical bonding of Lewis Theory |.

In 1916 W. Kossel together with G.N. Lewis set forrad the electronic theory of chemic bonding. It was suggested that inwards a chemic reaction, the atom of an chemical ingredient adjusts their electronic configuration to that of the nearest noble gas. The atoms larn 2 electrons, duplet configuration or 8 electron octet structure. For example, H, Li, together with Be acquire ns² and all other atoms tend to attain ns² np⁶ configuration. On the footing of this octet theory, the chemic bonds stimulate got been divided into the next iii types:

1. Ionic or Electrovalent Bond.
2. Covalent Bond.
3. Co-ordinate bond.

Ionic Bond.

The bond formed yesteryear the consummate transference of ane or to a greater extent than electrons from ane atom to or together with thus other atom is called the ionic or electrovalent bond. This is formed betwixt the elements of depression ionization potential values (i.e., elements of grouping I-A together with II-A) together with the elements amongst a high electron affinity values such every bit the chemical ingredient of Group Vi together with Vii-A.

Examples.

NaCl:

• Sodium loses ane electron to achieve the electronic configuration of neon,1s², 2s², 2p⁶.
  
• Chlorine gains ane electron to larn the electronic configuration of argon ( 1s² 2s² 2p⁶ 3s² 2p⁶)
  
• The oppositely charged ions formed inwards this agency are held together yesteryear the electrostatic forcefulness of attraction.
  

CaCl2:

• Calcium loses two-electron to form Ca²⁺ ions together with acquires electronic configuration of argon ( 1s² 2s² 2p⁶ 3s² 3p⁶)
  
• These 2 electrons are taken upwards yesteryear 2 chlorine atoms to form  ‎Cl⁻ ‎ions.
  
• Due to the electrostatic forcefulness of attraction, these ions pack themselves inwards a crystal lattice.
  

Covalent Bond.

"A bond formed yesteryear the usual sharing of electrons betwixt 2 atoms is called Covalent Bond". The atoms amongst aught or depression electronegativity differences commonly shape covalent bonds.

Examples:

Formation of H2:

• Two hydrogen atoms portion their electrons together with achieve locomote a configuration of helium, (1s²)
  

H2O Molecule:

• Two hydrogen atoms achieve the configuration of Helium (1s²) together with oxygen acquires Neon configuration (1s² 2s² 2p⁶), inwards the formation of H2O.
  
• Similarly, inwards the formation of NH3. each atom tends to larn element of group 0 configuration
  

Co-ordinate covalent Bond.

"A covalent bond inwards which both inwards electrons are donated yesteryear ane of the atoms is called Co-ordinate covalent bond. The atom which donates the electron couplet is called the donor atom together with the atom which accepts than for bond formation is called the acceptor. This bond is represented yesteryear an arrow that runs from donor to acceptor atom.

Examples:

Formation of NH+4 : 

• Lone couplet electron of nitrogen is donated to H⁺ to shape Co-ordinate covalent bond.
  

Formation of H3O+:

• Lone couplet of electron on oxygen forms a co-ordinate covalent bond with H⁺.
  

Surfactants Definition | Types Of Surfactants, Washing Activity |

Surfactants Definition.

Any chemical compound that reduces the surface tension of H2O when dissolved inward H2O or H2O solution is called surfactants. It affects interfacial tension betwixt 2 liquids together with increases the wetting together with cleaning mightiness of water.

Types of Surfactants.

"Surfactants" are of the next 2 types:

1. Soap.
2. Detergents.

Washing activity of Surfactants. The cleaning activity of both lather together with detergent is due to lowering of the surface tension. The Cleaning procedure consists of :

1. Thoroughly wetting the dirt together with the surface of the article existence washed.
2. Removing the dirt/grease from the surface, and
3. Maintaining the dirt/grease inward a stable solution or respite (detergent).

Since lather together with detergents increment the wetting mightiness of water, it tin to a greater extent than easily penetrate the fabrics together with larn to the dirt/grease spots. Each molecule of surfactant may last considered every bit a long chain. One cease of the chain is hydrophilic (water-loving), together with the other is hydrophobic (water-hating or dirt-loving). The dirt-loving ends are attracted to the solid/dirt particle together with environs it. At the same time, the H2O loving-ends clitoris the molecules together with the dirt particles away from the fabrics together with accept into the water.

This activity enables a lather or detergent to take dirt/grease particles from fabrics.

Soaps.

Soaps are molecules containing a rattling long alkyl grouping that is soluble inward crude together with an ionic cease (the common salt of a carboxylic acid) that is soluble inward water

In function, the hydrophobic part dissolves inward oils together with the hydrophilic cease (ionic end) dissolves inward water. Droplets of crude are hence emulsified together with removed. In addition, soaps lower the surface tension of H2O together with hence making it a amend wetting agent.

Detergents.

Synthetic detergent is structurally similar to soaps, differing inward primarily inward the water-soluble portion. They cause got the wages of existence able to business office inward difficult water. Some illustration is giving below:

Anion-active Detergents or Anioinic Detergents.

Cationic-active or Cationic Detergent.

A fourth ammonium salt

Non-ionic Detergent.

Detergents business office similar lather since 1 cease of molecules is oil-soluble together with the other cease is water-soluble.

Second Police Line Of Thermodynamics | Statements, Carnot Wheel |

Second Law of Thermodynamics.

The diverse statements of the second constabulary of thermodynamics are:

Clausius Statement.

"It is impossible to build a car which is able to choose estrus yesteryear a cyclic procedure from a reservoir at a lower temperature to i at a hotness unless run is done on the car yesteryear to a greater extent than or less external agency".

Example.

In a refrigerator, estrus from the inner compartment is transferred to the surround at a higher temperature at the expenditure of work.

Kelvin-Planck Statement.

"It is impossible to build a car that, operating inward a cyclic process, volition accept estrus from a reservoir at constant temperature in addition to convert it into run without accompanying changes inward the reservoir or its surroundings".

Lewis Statement.

"Every organisation that is left to itself will, on the average, alter towards a status of maximum probability".

"When a organisation undergoes a reversible change, the full entropy of the organisation in addition to surround remains constant, but when a organisation undergoes a natural spontaneous alter (irreversible) change, the full entropy of the organisation in addition to surrounding increase".

The Carnot Cycle.

To calculate the maximum extent to which estrus tin live on converted into work, Nicolas Sadi Carnot, a French pharmacist devised a hypothetical engine working inward a cyclic manner, inward 4 stages. These stages institute the Carnot cycle. The gas returns to its master copy Blue Planet at the terminate of the quaternary step.

In this machine, the working pith is i mole of an ideal gas in addition to it is contained inward a cylinder fitted amongst a frictionless in addition to weightless piston.

It is supposed that 2 really large reservoirs of estrus at T2 in addition to T1 are available. It is likewise possible to surround the cylinder yesteryear a perfect non-conductor, thus, adiabatic processes are possible.

First Step. (Isothermal Expansion)

The cylinder containing but 1 mole of gas of book V1 at pressure level P1 is placed inward the constant temperature reservoir at T2. Let the gas expands isothermally in addition to reversibly to the novel book V2, along AB.

The run W1 done yesteryear the gas afterwards taking estrus Q2 from the reservoir is given by

Second Operation. (Adiabatic Expansion)

At B the gas is at T2 in addition to has a book V2 nether the novel pressure level P2. It is straight off completely isolated in addition to is allowed to expand adiabatically along BC to novel book V3.

The run is done at the expense of the kinetic liberate energy of the gas molecules. Therefore, at that topographic point is a autumn of temperature from T2 to T1 in addition to the run done is

W2   = Cv  (T2 - T1)         ......... (ii) 

Third Operation. (Isothermal Compression)

The cylinder is straight off placed inward contact amongst a hot reservoir at T1 in addition to the gas is compressed isothermally in addition to reversibly from C to D: The concluding book is V4, in addition to so that the run is done is represented by

Where - Q1 is estrus given to the reservoir yesteryear gas at T1. In fact, W3 is negative because V3 is greater than V4 in addition to (iii) represents the run done on the gas inward compression.

Fourth Operation. (Adiabatic Compression)

The gas is i time again isolated in addition to compressed adiabatically along DA until the initial Blue Planet Influenza A virus subtype H5N1 is regained. The temperature of the gas rises from T1 to T2 and the book alter from V2  to V1. The run done upon the gas is 

W4   =   - Cv (T2 - T1)          ........... (iv)

The full run is done inward this four-stage performance is as:

W   =   W1  +  W2  - W3  + W4

Substituting the values,

Since V1 in addition to V4 prevarication on i adiabatic curve, in addition to V2 in addition to V3 are on another, it follows that

On substituting these inward (v), it is seen that

Dividing (vii) yesteryear (i) nosotros get

The constituent W/Q2 is called the thermodynamic efficiency of the reversible cycle. It gives the fraction of estrus which is possible to convert into work.

The Carnot equation (viii) reveals that the efficiency of a procedure depends upon the temperature limits betwixt which wheel operates in addition to is independent of the nature of the working pith in addition to other factors.